Dạng 1: nhờ vào bảng biến chuyển thiên với đồ thị để biện luận số nghiệm của phương trình
Bài toán: Biện luận số nghiệm của phương trình: F ( x m; )= 0 theo thông số m dựa vào đồ thị hoặc bảngbiến thiên của hàm số y = f ( x).Bạn đang xem: Biện luận số nghiệm của phương trình
Phương pháp giải:
bước 1: thay đổi phương trình F ( x m; )= 0 về dạng f ( x ) = g m( ). cách 2: Vẽ đồ gia dụng thị hoặc bảng biến đổi thiên của hàm số y = f ( x )( C)và đường thẳng d :y =g m( )Đường trực tiếp d có điểm sáng vuông góc cùng với trục tung và giảm trục tung tại điểm tất cả tung độ g m( ). cách 3: dựa vào đồ thị hoặc bảng thay đổi thiên của hàm số để biện luận số nghiệm của phương trình đã
cho.
Ví dụ 1: mang lại hàm số
4 2y = − x + 2 x gồm đồ thị như hình bên. Tìm kiếm tất cả
các cực hiếm thực của thông số m để phương trình
4 2− x + 2 x = mcó bốn
nghiệm thực phân biệt?
A. M > 0
B. 0 ≤ m≤ 1
C. 0 ví dụ 2: <Đề thi tìm hiểu thêm THPT QG năm 2019> mang đến hàm số y = f ( x)có bảng vươn lên là thiên như sau
x −∞ − 2 0 2 +∞
f ′ ( x) − 0 + 0 − 0 +f ( x )####### +∞ 1 +∞
####### − 2 − 2
Số nghiệm thực của phương trình 2 f ( x )+ 3 = 0 là####### A. 4 B. 3 C. 2 D. 1
Lời giải
Số nghiệm thực của phương trình ( ) ( )####### 3
####### 3 0
####### 2
f x f x
####### −
= ⇔ = đó là số giao điểm của trang bị thị hàm sốy = f ( x)và đường thẳng####### 3
####### 2
y = −.
Đường thẳng
####### 3
####### 2
y = − giảm đồ thị hàm số y = f ( x)tại 4 điểm phân biệt.Vậy phương trình 2 f ( x )+ 3 = 0 có đúng 4 nghiệm thực phân biệt. Lựa chọn A.Ví dụ 3: cho hàm số
3 2y = ax + bx + cx + d tất cả đồ thị trong hình bên.
Hỏi phương trình
3 2ax + bx + cx + d+ 1 = 0 có bao nhiêu nghiệm?
A. Phương trình không có nghiệm.
B. Phương trình gồm đúng 1 nghiệm.
C. Phương trình gồm đúng 2 nghiệm.
D. Phương trình tất cả đúng 3 nghiệm.
Lời giải
Số nghiệm của phương trình sẽ cho phụ thuộc vào số giao điểm của thứ thị hàm số
( )3 2y = ax + bx + cx + d C và đường thẳng y = − 1.
Dựa vào đồ dùng thị ta thấy ( C ) cắt đường trực tiếp y = − 1 tại 3 điểm phân biệt nên phương trình đang cho bao gồm 3nghiệm. Chọn D.
Ví dụ 4: Tìm tất cả các giá trị m để phương trình
3x − 3 x = 2 mcó 3 nghiệm phân biệt
A. − 2 ví dụ như 7: cho hàm số ( )
4 2y = f x = x − 2 x + 2 tất cả bảng thay đổi thiên như sau
x −∞ − 1 0 1 +∞
y′ − 0 + 0 − 0 +
y
####### +∞ 2 +∞
####### 1 1
Số cực hiếm nguyên của m để phương trình
4 22 x − 4 x + m− 5 = 0 bao gồm đúng 2 nghiệm
####### A. 3 B. 4 C. 5 D. 6
Lời giải
Ta có: PT ( )####### 4 2 5 4 2 9
####### 2 2 2 2
####### 2 2
m mx x x x
####### − −
####### ⇔ − = ⇔ − + =
Số nghiệm của phương trình (2) là số giao điểm của vật dụng thị ( C )và con đường thẳng####### 9
####### 2
my
####### −
####### =
Do vậy phương trình đã cho bao gồm 2 nghiệm ⇔ d giảm ( C )tại 2 điểm phân biệt####### 9
####### 1
####### 2 7
####### 9 5
####### 2
####### 2
m
m
m m
####### −
####### =
####### =
####### ⇔ ⇔
#######
####### −
#######
Kết hợp m m 1; 2;3; 4;5;7 ∈ ⇒ =. Lựa chọn D.Ví dụ 8 : Tìm toàn bộ các quý giá thực của tham ốs m làm sao để cho đường trực tiếp y = m giảm đồ thị hàm số
3y = x − 3 x+ 1 tại 3 điểm phân biệt, trong những số ấy có đúng hai điểm phân biệt tất cả hoành độ dương.
A. − 1 3 D.
####### 1 5
####### 2 2
Ví dụ 11: đến hàm số ( )
3 2y = f x = − x − 3 x + 4 tất cả bảng trở thành thiên như sau
x −∞ − 2 0 +∞
y′ − 0 + 0 −
y
####### +∞ 4
####### 0 −∞
Phương trình
3 2x + 3 x + 2 m= 0 , cùng với m là thông số thực, bao gồm 3 nghiệm thực khác nhau khi m trực thuộc tập hợp
nào bên dưới đây?
Ví dụ 14: mang lại hàm số ( )3 2y = f x = − x − 3 x + 4 bao gồm bảng biến chuyển thiên như sau
x −∞ − 2 0 +∞
y′ − 0 + 0 −
y
####### +∞ 4
####### 0 −∞
Phương trình
3 2x + 3 x + 2 m= 0 , cùng với m là thông số thực, bao gồm 3 nghiệm thực phân minh khi m trực thuộc tập hợp
nào bên dưới đây?
A. < −2;0 > B. ( −2;0 ) C. < −3; − 2 > D. < −2;0>Lời giải
PT ( )3 2⇔ − x − 3 x + 4 = 2 m+ 4 . Phương trình () là phương trình hoành độ giao điểm của đường thẳng
y = 2 m+ 4 cùng đồ thị hàm số ( )3 2y = f x = −x − 3 x + 4. Phương trình tất cả 3 nghiệm phân minh khi hai vật thị
có 3 giao điểm. Lúc đó 0 ví dụ như 15: mang đến đồ thị hàm số ( )4 2y = f x = − x + 2 x + 3
như hình vẽ. Số các giá trị nguyên của tham số
m ∈ − < 10;10 > nhằm phương trình4 2 4 2x − 2 x = m − 2 m có
đúng 2 nghiệm riêng biệt là
####### A. 17
####### B. 18
####### C. 19
####### D. 20
Lời giải
Ta có: ( )4 2 4 2 4 2 4 2x − 2 x = m − 2 m ⇔ − x + 2 x + 3 = −m + 2 m +3 *
Dựa vào đồ vật thị hàm số ta thấy: Phương trình (*) có đúng nhị nghiệm phân biệt
4 2
####### 2
####### 2 3 3
####### 2
mm m
m
#######
Kết hợp
m < 10;10>m
####### ∈ −
####### ⇒
####### ∈
có 18 quý hiếm của thông số m. Lựa chọn B.
Ví dụ 16: cho hàm số
3 2
y = x − 6 x + 9 x + m (với m là tham số thực) tất cả đồ thị ( C ). Mang sử ( C )cắt trụchoành trên 3 điểm phân biệt có hoành độ x 1 , x 2 ,x 3 (với x 1 Đồ thị ( C )cắt trục hoành tại bố điểm phân biệt.
Khi kia PT
3 2x − 6 x + 9 x + m= 0 có bố nghiệm phân biệt.
Suy ra PT
3 2x − 6 x + 9 x = − mcó tía nghiệm phân biệt, suy ra
đường trực tiếp y = − mcắt vật thị hàm số
3 2y = x − 6 x + 9 xtại 3
điểm phân biệt.
Ta gồm đồ thị nhì hàm số như hình bên.
Hai đồ dùng thị có 3 giao điểm khi và chỉ khi − 4 những phép tịnh tiến đồ gia dụng thị hàm số
Trong phương diện phẳng tọa độ Oxy , mang đến đồ thị ( C )của hàm số y = f ( x), p và q là hai số dương tùy ý. Khi
đó:
Tịnh tiến ( C )lên bên trên q đơn vị thì ta được đồ thị của hàm số y = f ( x )+ q.
Tịnh tiến ( C )xuống bên dưới q đơn vị thì ta được đồ gia dụng thị của hàm số y = f ( x) − q.
Tịnh tiến ( C )sang trái p đơn vị thì ta được đồ vật thị của hàm số y = f ( x + p).
Tịnh tiến ( C )sang phải p đơn vị chức năng thì ta được vật dụng thị của hàm số y = f ( x − p).
Một số phép suy trang bị thị chủng loại 1: đến đồ thị hàm số y = f ( x)( C )thì vật dụng thị hàm số y = f ( x) gồm 2 phần.Phần 1: Là phần đồ thị hàm số ( C )nằm phía trên trục hoành.
Phần 2: đem đối xứng phần của ( C )nằm bên dưới Ox qua Ox.
Phần 1: Là phần đồ dùng thị hàm số ( C )nằm phía bên trên trục hoành.Phần 2: rước đối xứng phần của ( C )nằm dưới Ox qua Ox.Dựa vào vật dụng thị hàm số (hình vẽ bên) để con đường thẳng y = mcắt vật thị ( C )tại 6 điểm riêng biệt khi với chỉkhi 2 Ta có: PT ( )
3⇔ − x + 3 x + 1 = 2 − m* ⇒ Phương trình (*)
là phương trình hoành độ giao điểm vật dụng thị hàm số
3y = 3 x − x + 1 và đường thẳng y = 2 − m vuông góc với
trục tung. Phương trình vẫn cho tất cả sáu nghiệm phân biệt
khi còn chỉ khi hai thứ thị cắt nhau trên 6 điểm phân biệt. Ta
có vật dụng thị nhị hàm số như hình bên. Để hai thứ thị cắt nhau
tại 6 điểm thì 0 ví dụ 4: đến hàm số y = f ( x)có đồ vật thị như hình mẫu vẽ bên. Số nghiệmthực của phương trình 2 f ( x )+ 1 = 5 là:
####### A. 3
####### B. 5
####### C. 2
####### D. 4
Lời giải
Ta có: ( )( )( )( )( )####### 2 1 5 2
####### 2 1 5
####### 2 1 5 3
f x f xf xf x f x
####### + = =
####### + = ⇔ ⇔
####### + = − = −
#######
Dựa vào đồ thị hàm số ta thấy, phương trình f ( x ) = 2 gồm 2 nghiệm với phương trình f ( x ) = − 3 có mộtnghiệm đề nghị phương trình vẫn cho gồm 3 nghiệm. Lựa chọn A.
Ví dụ 5: cho hàm số y = f ( x)có thứ thị như hình vẽ bên. Số nghiệmthực của phương trình 2 f ( x )+ 3 = 8 là:####### A. 7
####### B. 5
####### C. 4
####### D. 6
Lời giải
Ta có: ( )( )( )( )( )####### 5
####### 2 3 8
####### 2
####### 2 3 8
####### 2 3 8 11
####### 2
f xf xf xf xf x
#######
####### =
####### + =
####### + = ⇔ ⇔
####### + = − −
####### =
#######
Dựa vào đồ vật thị hàm số ta thấy, phương trình ( )####### 5
####### 2
f x = có 4 nghiệm và phương trình ( )####### 11
####### 2
f x
####### −
= có 2
nghiệm yêu cầu phương trình đã cho tất cả 6 nghiệm. Chọn D.
Ví dụ 6: Hình bên là vật dụng thị hàm số
4 2y = 2 x − 4 x + 1. Tìm toàn bộ các
giá trị của thông số m nhằm phương trình
####### 4 2 1
####### 2 2
####### 2
x − x + = m gồm 8
nghiệm phân biệt
####### A.
####### 1
####### 0
####### 2
Gọi ( )
4 2y = 2 x − 4 x + 1 C
Đồ thị hàm số
4 2y = 2 x − 4 x + 1 có 2 phần:
Phần 1: Là phần vật dụng thị hàm số ( C ) ở phía bên trên trụchoành.
Phần 2: đem đối xứng phần của ( C )nằm bên dưới Ox qua Ox.Dựa vào thiết bị thị hàm số
4 2y = 2 x − 4 x + 1 và con đường thẳng y = 4 m suy ra phương trình vẫn cho có 8
nghiệm riêng biệt khi và chỉ khi hai thiết bị thị tất cả 8 giao điểm. Hai đồ dùng thị có 8 giao điểm
Phương trình f ( x )= mlà phương trình hoành độ giao điểm củađồ thị hàm số y = f ( x) và con đường thẳng y = m song song trụchoành bao gồm đồ thị nghỉ ngơi hình bên. Hai trang bị thị tất cả bao nhiêu giao điểm thì
PT f ( x )= mcó bấy nhiêu nghiệm.m ∈ ( 1;3)thì hai thiết bị thị tất cả 4 giao điểm, suy ra PT f ( x )= mcó4 nghiệm. Lựa chọn A.
Ví dụ 9 : cho hàm số ( ) ( ) ( )
2y = f x = x + x − 2 .g x có đồ thị như
hình vẽ. Hotline S là tập hợp những giá trị nguyên của m nhằm phương trình
( )2x + x − 2 .g x = m có 3 nghiệm phân biệt. Tổng các thành phần của
S là:
####### A. 4
####### B. 6
####### C. − 6
####### D. − 4
Lời giải
Ta có:
####### 2 1
####### 2 0
####### 2
xx xx
####### ≥
####### + − ≥ ⇔
####### ≤ −
Gọi ( ) ( ) ( )( )
2y = f x = x + x − 2 .g x C thì trang bị thị hàm số
( )2y = x + x − 2 .g x có 2 phần.
Xem thêm: Biện luận công thức máu ) - biện luận cận lâm sàng(công thức máu)
Phần 1: Là phần của ( C )ứng cùng với miền####### 1
####### 2
x
x
####### ≥
#######
####### ≤ −
Phần 2: đem đối xứng phần ( C ) ứng với miền − 2hoành.
Dựa vào vật dụng thị hàm số suy ra phương trình ( )2x + x − 2 .g x = mcó 3 nghiệm sáng tỏ khi − 4 phối kết hợp m ∈ ⇒ m= −3; −2; − 1 ⇒ tổng các thành phần của S là − 6. Chọn C.
x −∞ − 2 3 +∞
y′ + 0 − 0 +
Ví dụ 10 : mang lại hàm số y = f ( x)có bảng biến đổi thiênnhư hình vẽ. Số nghiệm của phương trình
f ( x − 1 ) = 2 là####### A. 4 B. 5
####### C. 2 D. 3
y
####### 4 +∞
####### −∞ − 2
Lời giải
Ta tất cả đồ thị hàm số y = f ( x)có dạng như hình sau:Đồ thị hàm số y = f ( x − 1 )( C)là đồ dùng thị hàm số y =f ( x)khi dịch sang buộc phải 1 đơn vị chức năng (xem hình 1).
Đồ thị hàm số y = f ( x− 1 ) là có 2 phần (xem hình 2)Phần 1: Là phần của ( C )nằm trên trục hoànhPhần 2: rước đối xứng phần nằm dưới trục hoành của ( C )qua Ox.Dựa vào thứ thị hàm số y = f ( x− 1 ) suy ra phương trình f ( x − 1 ) = 2 có 5 nghiệm. Lựa chọn B.Đồ thị hàm số y = f ( x − 1 )( C)là đồ thị hàm số y = f ( x)khi dịch sang đề nghị 1 đơn vị (hình 1)Đồ thị hàm số y = f ( x− 1 )gồm 2 phần:Phần 1: Là phần của ( C )nằm bên đề xuất trục tung.Phần 2: Hàm số y = f ( x− 1 )là hàm chẵn, ta mang đối xứng phần 1 qua trục tung (hình 2).Dựa vào hình 2 suy ra phương trình f ( x − 1 )= mcó 4 nghiệm rõ ràng khi − 1 cùng với m ∈ ⇒ m=0;1; 2 . Lựa chọn A.
Dạng 3: các bài toán áp dụng đồ thị kết hợp phương thức đặt ẩn phụ
Bài toán: mang đến hàm số y = f ( x). Biện luận số nghiệm của phương trình f u x ( ) =m#######
####### .
Phương pháp giải:
bước 1: Đặt t = u x( )ta cần xác định miền quý hiếm của t và khớp ứng với mỗi giá trị của t tất cả bao nhiêugiá trị của x.
(Ta hoàn toàn có thể lập bảng đổi mới thiên hàm số t = u x( )để thừa nhận xét cùng tìm miền của t ). cách 2: dựa vào đồ thị, biện luận số nghiệm của phương trình f ( )t = mtừ đó suy ra số nghiệm củaphương trình f u x ( ) =m#######
####### .
Ví dụ 1: <Đề thi tìm hiểu thêm năm 2018> mang lại hàm số y =f ( x)liên tục bên trên và gồm đồ thị như mẫu vẽ bên. Tập hợp toàn bộ các
giá trị thực của tham số m để phương trình f ( sinx )= m cónghiệm thuộc khoảng tầm ( 0; π ) làA. < −1;3)B. ( −1;1)
C. ( −1;3)
D. < −1;1)
Lời giải
Đặt t = sinx, cùng với x ∈ ( 0; π) ⇒ t∈ ( 0;1>. Lúc ấy f ( sinx ) = m ⇔ f ( )t = m.
Dựa vào thứ thị hàm số, để f ( )t = mcó nghiệm trực thuộc ( 0;1> ⇔ − 1 ≤ m 0Theo bất đẳng thức Cosi ta có: ( )
####### 1 1
####### 1
####### 2 2
x xx x
####### + −
####### − ≤ =
Do đó
2
1 ≤ t ≤ 2 ⇒ 1 ≤ t≤ 2. Vậy x ∈ < 0;1> ⇒ t ∈ 1; 2
#######
Ta có: f ( ) 1 = −1, f( 2 )= 2 2 − 5
Kết hợp vật thị suy ra phương trình f ( )t = mcó nghiệm nằm trong đoạn 1; 2
#######
thì m ∈ 2 2 − 5; − 1
Vậy tất cả 2 quý hiếm nguyên của m ∈ − 2; − 1 để phương trình đang cho có nghiệm. Lựa chọn A.
Ví dụ 3: cho hàm số ( )
4 2y = f x = − x + 2 x thường xuyên trên cùng có
đồ thị như hình vẽ bên. Số những giá trị nguyên của thông số m để
phương trình ( ) ( )
4 2− 1 − sin x + 2 1 − sinx = mcó nghiệm là:
####### A. 2 B. 8
####### C. 3 D. 9
Lời giải
Đặt t = 1 − sinx ta có: sin x ∈ −< 1;1 > ⇒ t∈< 0; 2>
Ta có: f ( 2 )= − 8. Dựa vào đồ thị hàm số ta thấy t ∈ < 0; 2> ⇒ f ( )t ∈ −< 8;1>
Vậy phương trình ( ) ( )
4 2
− 1 − sin x + 2 1 − sinx = mcó nghiệm lúc m ∈ −< 8;1>
Ví dụ 6: mang đến hàm số ( )4 2y = f x = − x + 2 x + 1 bao gồm đồ thị như mẫu vẽ bên. Số
giá trị nguyên của m nhằm phương trình f f ( x ) =m#######
có nghiệm x ∈ −< 1;1 >.####### A. 10 B. 11
####### C. 12 D. 13
Lời giải
Dựa vào thiết bị thị hàm số ta thấy cùng với x ∈ −< 1;1 > ⇒ f ( x) ∈<1; 2 >Đặt t = f ( x), xét phương trình f ( )t = mvới t ∈<1; 2 >Dựa vào đồ gia dụng thị hàm số với t ∈< 1; 2> ⇒ f ( )t ∈ −< 7; 2>Do kia phương trình f f ( x ) =m#######
có nghiệm x ∈ −< 1;1 > ⇔ m∈ −< 7; 2>Kết đúng theo m ∈ ⇒có 10 quý hiếm của m. Lựa chọn A.
Ví dụ 7: mang lại hàm số
####### 1
####### 1
xyx
####### +
####### =
####### −
có thứ thị như hình vẽ. Kiếm tìm m để
phương trình
sin 1
sin 1
x mx
####### +
####### =
####### −
có nghiệm ; 2
x
π ∈ −
A. M ∈ −< 1;0 > B. M ∈ −< 1;0)C. M ∈ −< 1; +∞ ) D. M ∈ −( 1;0>Lời giải
Ta có: ;0 sin < 1;0)####### 2
x x
π ####### ∈ − ⇒ ∈ −
#######
#######
. Đặt
####### 1
sin 1
tt x mt
####### +
####### = ⇒ =
####### −
với t ∈ −< 1;0)Dựa vào đồ dùng thị hàm số ta thấy phương trình f ( )t = mcó nghiệm t ∈ −< 1;0 ) ⇔ m∈ −( 1;0 >. Chọn D.Ví dụ 8 : mang đến hàm số y = f ( x)có đạo hàm bên trên và tất cả bảng biến hóa thiên như hình vẽ bên dưới đâyx −∞ − 1 1 +∞
y′ + 0 − 0 +
y
####### 2 +∞
####### −∞ 0
Số nghiệm của phương trình f ′ f ( x) = 0#######
là:
####### A. 4 B. 7 C. 6 D. 3
Lời giải
Đặt g ( x ) = f f ( x)#######
ta có: ( ) ( ) ( )( )( )####### 0
####### . 0
####### 0
f x
g x f x f f x f f x
####### ′ =
####### ′ = ′ ′ = ⇔
#######
####### ′ =
#######
Dựa vào đồ thị hàm số ta thấy ( ) ( )####### 1
####### 0 0
####### 1
xf x f xx
####### = −
####### ′ = ⇔ ⇒ ′ =
#######
####### =
có 2 nghiệm phân minh x = ± 1.
Lại có: ( )( )( )####### 1
####### 0
####### 1
f x
f f x f x
####### = −
####### ′ = ⇔
#######
####### =
#######
Phương trình f ( x ) = − 1 gồm một nghiệm duy nhấtPhương trình f ( x ) = 1 tất cả 3 nghiệm phân biệt.Do kia phương trình g ′ ( x) = 0 gồm 6 nghiệm phân biệt. Chọn C.
Phương trình bậc 2 một ẩn là giữa những kiến thức quan trọng đặc biệt trong lịch trình toán trung học cơ sở. Vày vậy, lúc này Kiến Guru xin trình làng đến chúng ta đọc bài viết về chủ đề này. Bài viết sẽ tổng vừa lòng các triết lý căn bản, đồng thời cũng chuyển ra phần đa dạng toán thường gặp mặt và những ví dụ áp dụng một phương pháp chi tiết, rõ ràng. Đây là chủ đề ưa chuộng, hay lộ diện ở những đề thi tuyển sinh. Cùng Kiến Guru tìm hiểu nhé:
Phương trình bậc 2 một ẩn - Lý thuyết.
Phương trình bậc 2 một ẩn là gì?
Cho phương trình sau: ax2+bx+c=0 (a≠0), được call là phương trình bậc 2 với ẩn là x.
Công thức nghiệm: Ta call Δ=b2-4ac.Khi đó:
Δ>0: phương trình sống thọ 2 nghiệm:.
Trong trường hòa hợp b=2b’, để dễ dàng ta có thể tính Δ’=b’2-ac, tựa như như trên:
Δ’>0: phương trình bao gồm 2 nghiệm phân biệt.
Định lý Viet và ứng dụng trong phương trình bậc 2 một ẩn.
Cho phương trình bậc 2 một ẩn: ax2+bx+c=0 (a≠0). đưa sử phương trình có 2 nghiệm x1 cùng x2, hôm nay hệ thức sau được thỏa mãn:

Dựa vào hệ thức vừa nêu, ta có thể sử dụng định lý Viet để tính những biểu thức đối xứng chứa x1 cùng x2
x1+x2=-b/ax12+x22=(x1+x2)2-2x1x2=(b2-2ac)/a2…Nhận xét: Đối với dạng này, ta cần chuyển đổi biểu thức sao cho xuất hiện tại (x1+x2) với x1x2 để vận dụng hệ thức Viet.
Định lý Viet đảo: giả sử tồn tại nhị số thực x1 và x2 thỏa mãn: x1+x2=S, x1x2=P thì x1 và x2 là 2 nghiệm của phương trình x2-Sx+P=0
Một số ứng dụng thường gặp gỡ của định lý Viet vào giải bài tập toán:
Nhẩm nghiệm phương trình bậc 2: mang đến phương trình ax2+bx+c=0 (a≠0),Nếu a+b+c=0 thì phương trình gồm nghiệm x1=1 cùng x2=c/aNếu a-b+c=0 thì phương trình bao gồm nghiệm x1=-1 cùng x2=-c/a
Phân tích nhiều thức thành nhân tử: đến đa thức P(x)=ax2+bx+c giả dụ x1 và x2 là nghiệm của phương trình P(x)=0 thì đa thức P(x)=a(x-x1)(x-x2)Xác định dấu của các nghiệm: đến phương trình ax2+bx+c=0 (a≠0), mang sử x1 và x2 là 2 nghiệm của phương trình. Theo định lý Viet, ta có:

II. Dạng bài tập về phương trình bậc 2 một ẩn:
Dạng 1: bài xích tập phương trình bậc 2 một ẩn không xuất hiện tham số.
Để giải các phương trình bậc 2, cách phổ biến nhất là thực hiện công thức tính Δ hoặc Δ’, rồi áp dụng những điều kiện và công thức của nghiệm đã làm được nêu sinh hoạt mục I.
Ví dụ 1: Giải những phương trình sau:
x2-3x+2=0x2+x-6=0Hướng dẫn:
Δ=(-3)2-4.2=1. Vậy
Ngoài ra, ta có thể áp dụng phương pháp tính nhanh: lưu ý

suy ra phương trình bao gồm nghiệm là x1=1 và x2=2/1=2
Δ=12-4.(-6)=25. Vậy
Tuy nhiên, ngoài những phương trình bậc 2 đầy đủ, ta cũng xét đa số trường hợp quan trọng đặc biệt sau:
Phương trình khuyết hạng tử.Khuyết hạng tử bậc nhất: ax2+c=0 (1).
Phương pháp:


Khuyết hạng tử tự do: ax2+bx=0 (2). Phương pháp:

Ví dụ 2: Giải phương trình:
x2-4=0x2-3x=0Hướng dẫn:
x2-4=0 ⇔ x2=4 ⇔ x=2 hoặc x=-2x2-3x=0 ⇔ x(x-3)=0 ⇔ x=0 hoặc x=3Phương trình đem đến dạng bậc 2.Phương trình trùng phương: ax4+bx2+c=0 (a≠0):
Đặt t=x2 (t≥0).Phương trình đã mang lại về dạng: at2+bt+c=0Giải như phương trình bậc 2 bình thường, chăm chú điều khiếu nại t≥0Phương trình cất ẩn ở mẫu:
Tìm điều kiện khẳng định của phương trình (điều khiếu nại để chủng loại số khác 0).Quy đồng khử mẫu.Giải phương trình vừa nhấn được, để ý so sánh với điều kiện ban đầu.Chú ý: phương pháp đặt t=x2 (t≥0) được gọi là cách thức đặt ẩn phụ. Ngoài đặt ẩn phụ như trên, so với một số bài xích toán, cần khéo léo lựa chọn làm thế nào để cho ẩn phụ là tốt nhất có thể nhằm đưa bài toán từ bậc cao về dạng bậc 2 thân quen thuộc. Ví dụ, rất có thể đặt t=x+1, t=x2+x, t=x2-1…
Ví dụ 3: Giải các phương trình sau:
4x4-3x2-1=0
Hướng dẫn:
Đặt t=x2 (t≥0), từ bây giờ phương trình trở thành:4t2-3t-1=0, suy ra t=1 hoặc t=-¼
t=1 ⇔ x2=1 ⇔ x=1 hoặc x=-1.t=-¼ , các loại do điều kiện t≥0Vậy phương trình có nghiệm x=1 hoặc x=-1.
Ta có: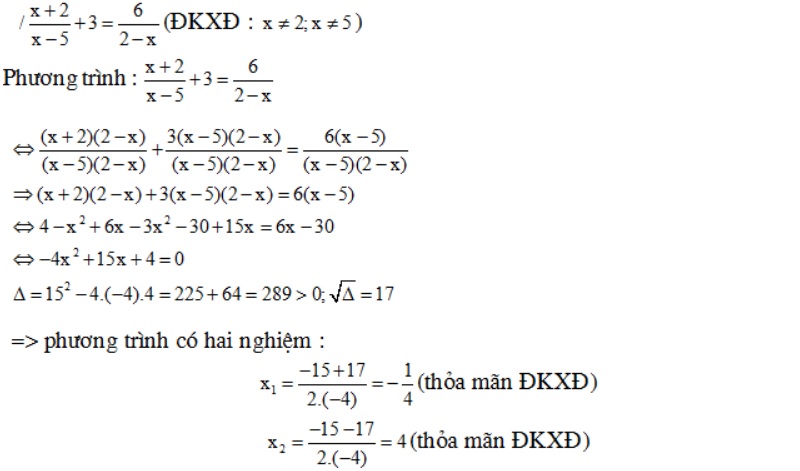
Dạng 2: Phương trình bậc 2 một ẩn bao gồm tham số.
Biện luận số nghiệm của phương trình bậc 2.Phương pháp: áp dụng công thức tính Δ, dựa vào dấu của Δ để biện luận phương trình gồm 2 nghiệm phân biệt, tất cả nghiệm kép xuất xắc là vô nghiệm.
Ví dụ 4: Giải với biện luận theo thông số m: mx2-5x-m-5=0 (*)
Hướng dẫn:
Xét m=0, khi đó (*) ⇔ -5x-5=0 ⇔ x=-1
Xét m≠0, lúc đó (*) là phương trình bậc 2 theo ẩn x.


Phương pháp: nhằm nghiệm thỏa yêu cầu đề bài, trước hết phương trình bậc 2 phải bao gồm nghiệm. Vị vậy, ta tiến hành theo công việc sau:
Tính Δ, tìm điều kiện để Δ không âm.Dựa vào định lý Viet, ta tất cả được các hệ thức thân tích cùng tổng, từ kia biện luận theo yêu ước đề.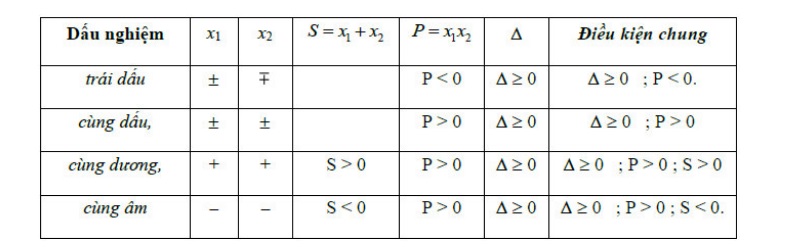
Ví dụ 5: mang lại phương trình x2+mx+m+3=0 (*). Tìm m nhằm phương trình (*) có 2 nghiệm thỏa mãn:

Hướng dẫn:
Để phương trình (*) có nghiệm thì:

Khi đó, gọi x1 cùng x2 là 2 nghiệm, theo định lý Viet:

Mặt khác:

Theo đề:

Thử lại:
Khi m=5, Δ=-7 lúc m=-3, Δ=9 >0 (nhận)vậy m = -3 thỏa yêu mong đề bài.
Trên đây là tổng hòa hợp của con kiến Guru về phương trình bậc 2 một ẩn. Mong muốn qua bài viết, các các bạn sẽ hiểu rõ hơn về chủ thể này. Ngoài bài toán tự củng cố kiến thức cho phiên bản thân, chúng ta cũng sẽ rèn luyện thêm được bốn duy xử lý các việc về phương trình bậc 2. Các bạn cũng tất cả thể bài viết liên quan các nội dung bài viết khác bên trên trang của loài kiến Guru để mày mò thêm nhiều kỹ năng mới. Chúc các bạn sức khỏe với học tập tốt!









